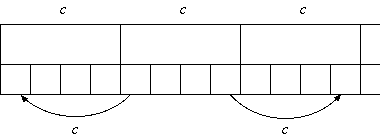
図1
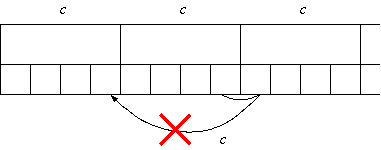
図2
線形加速定理は、一ステップに処理する情報量を何倍にもして計算速度を速く するというものです。 ここでは与えられた Turing 機械 を 倍速く計算する Turing 機械 を作ることを考えます。 以下、そのような Turing 機械の構成を示しますが、簡単のため 1 テープ Turing 機械の構成のみを示します。
新しく作る Turing 機械 では の ステップの計算を 6 ステップで行うようにします。 そのためにまず必要なのは、テープの一マスに書き込める記号の数を、 の 乗とし、 のテープ マス分の情報を 1 マスに書けるようにします。 これを以下大きいマスと呼ぶことにします。
さて、テープをこのように マス分を 1 マス分に書くようにし ておいて、 の ステップを 6 ステップでシミュレートすることを考えます。 6 ステップの内訳は、最初の 4 ステップで現在のヘッドの位置の両隣の大き なマスの内容を収集して、次の 2 ステップで ステップ分の 大きなマスの内容の変化を書き込みます。
マス分のテープの内容が 1 マスに書かれていますが、このうち もともと のヘッドがどこを読んでいたかは 個のラベル(状態)で記憶しておきます。 さて、 ステップ後にテープはどのようになっているかを考えます。 高々 マスしか動かないので、現在のヘッドの位置から左右に マスが最大の移動距離になります。 しかし、 マス分を 1 マスに書いた時、シミュレートしている のヘッドは最大でも隣の マスの中までしか到達しません(図1)。 またヘッドが動く経路を考えると両隣のマスに ステップ内に訪れることはできず、 現在の大きな 1 マスとどちらかの隣の大きな 1 マスだけを訪れることができ ます(図2)。


そこで、両隣の大きなマスの内容を収集し、 ステップシミュレーションをすると、中央のマスの内容とどちらか隣の大きな マスの内容が書き変わることになります。
ところで、両隣の大きな 3 マス分のテープの内容をあらかじめあらゆる状況 を想定しておけます。そして、それを読んで ステップ の内容をシミュレートするのもあらかじめやっておくことができます。 つまり、 ( のヘッドの位置)と(大きな 3 マス分のテープ内容) から ( を ステップシミュレートした結果の状態、ヘッド位置、テープ内容) はあらかじめ関数として計算できるわけで、 はこれをδ関数と して取り込むことができます。 つまり、このシミュレーション自体は 1 step で可能なわけです。
結局まとめると の ステップは次の 6 ステップでシミュレーションできます。
なお、加速定理と呼ばれるものもあります (証明は難しいけど、実用上意味がないので割愛します)。 以下のように、いくらでも加速できる(つまり最適なアルゴリズムの存在しな い)関数が存在すると言うものです。
次の条件を満たす計算可能関数 が存在します。
どんな増加関数 に対しても、 有限の場合を除き、 ステップ以内に を計算する Turing 機械が構成できる。
ここでは計算時間をかけないと解けない問題が存在することを示します。 はじめにこれに必要な補題をまとめます。
時間計算量 の任意の Turing 機械のコードを でシミュレートする万能 1 テープ Turing 機械が存在する。
これは万能 Turing 機械の構成で証明の概略を説明しました。 さらに 2 テープ Turing 機械では、次が言えました。
時間計算量 の任意の Turing 機械のコードを でシミュレートする万能 2 テープ Turing 機械が存在する。
さらに同じ関数を計算するプログラムが無限に存在するという次の補題 を使用します。
一つの計算可能な関数に対して、それを計算する Turing 機械は無限個存在す る。
これはプログラムの先頭などに、何もしない動作を埋め込むことで簡単に示す ことができます。 一方、次の補題は参考文献において階層定理を証明するのに使われています。
計算可能な関数を Turing 機械で実現するとき、有限の場合を除いて任意の長 さのコードを作ることができる。
この補題に関しては、参考文献では Turing 機械のコードの頭に 0 を埋め込 むことをゆるすことで示しています。 しかしこれを許すか許さないかはコンピュータのモデル化やコード化に依存し そうです。 但し、こちらを認めた方が良い結果が得られます。
関数のオーダーとして の表記を使用してきました。 が、ここでは付け加えて の表記を定義します。 は、 の増え方は よりも真に少ないことを意味し、ある意味 のような意味を持ちます。 この記号の厳密な定義は次の通りです。
「どのような定数 に対してもある数 が存在し、全ての より大きい数 に対して が成り立つ」。 なお、これは一階述語論理式では次のように書けます。
なお、 と は同値ではありません。
これらの補題を組み合わせることで次の階層定理が主張できます。
が時間構成可能関数だと仮定する。 また とする。 その時、 どんな時間計算量 の Turing 機械にも計算できない、時間計算量 で計算できる関数 が存在する。
が時間構成可能関数だと仮定する。 また とする。 その時、 どんな時間計算量 の Turing 機械にも計算できない、時間計算量 で計算できる関数 が存在する。
が時間構成可能関数だと仮定する。 また とする。 その時、どんな時間計算量 の Turing 機械にも計算できない、時間計算量 で計算できる関数 が存在する。
が時間構成可能関数だと仮定する。 また とする。 その時、どんな時間計算量 の Turing 機械にも計算できない、時間計算量 で計算できる関数 が存在する。
ここでは 6-1-b, 6-2-a を使用したものに対して証明することにします。
註: この が時間構成可能とは、 与えられた に対して、 step ちょうどで停止する Turing 機械を構成できると言うことです。 通常の増加関数はほぼ可能です。
関数 は入力 に対して次の処理をします。
この関数を計算するのに ステップかかるのは明らかです。 一方、 が ステップで計算できないことを示します。 を ステップで計算する Turing 機械 が存在すると仮定して矛盾を導きます。 もし が存在するのであれば、そのコード が存在 します。そのとき を考えます。 が成り立てば、 の計算においてシミュレートされ、値を出すことになり、対角線論法により矛盾を導けます。 しかし、与えられた条件はこれを満たすほど強力ではないため、この条件は満 たされる保証がありません。
ところが、補題 6-2-a により、 が計算可能である場合、それを計算する Turing 機械は無限個存在しますので、そのコードを とします。 が成り立つ時、どんな係数 に対しても有限の場合を除きすべて の において次が成り立ちます。
したがって、これを満たすような において、シミュレーションが最後まで実行できるため、対角線論法により矛盾が導けます。
いままで Turing 機械の計算ステップに関して、いろいろ議論してきましたが、 これらのことはテープの消費量に関しても同様になりたちます。 これを領域計算量と言います。
領域計算量 の テープ Turing 機 械を万能 Turing 機械でシミュレートする時、 の領域計算量で計算できます。
線形加速定理に対して、同様の証明で領域節約定理が成り立ちます。 但し、領域節約定理では実際に使用するテープのマスは減っても処理に必要な ビット数は変わりません。
階層定理は次が成り立ちます。
が領域構成可能関数だと仮定する。 また とする。 その時、 どんな領域計算量 の Turing 機械 にも計算でき ない、領域計算量 で計算できる関数 が存在する。
ここで領域構成可能関数とは、与えられた関数 に対して、すべてのパラメータ に対し、ちょうど マスだけ使用して停止する Turing 機械を構成できることを言います。
但しこれを証明するには、新しい概念と、補題が必要になります。 様相(Configuration) とは、Turing 機械の状態とテープヘッドの 位置と一回でも使用したテープの内容の組を指します。 テープの長さは無限を仮定していますが、有限時間内に使用するテープの量は 有限ですので、様相の長さは有限になります。 一方、δ関数により、ある様相から 1 ステップで行ける様相を 定義することが出来るます。すると、様相の集合を考えた時、計算を様相から 様相への移り替わりの列と定義することが出来、また、様相を頂点とすると、 δ関数で遷移できると言う関係を辺で表す有効グラフを定義できます。 今回、様相を用いることで使用するのは次の補題です。
Turing 機械 の領域の使用量が で抑えられてい るとする。 その時、 時間で が停止するかしないかを決定できるような定数 が存在する。
領域が で抑えられている時、様相の表現の長さも の定数倍 で抑えることが出来ます。 ここで、一般性を失わず、様相が 0, 1 だけで表現されていると仮定できます。 すると、表現可能な様相全ては高々 個だけになります。
Turing 機械 の計算を考えると、初期様相からスタートし、δ 関数に従って、様相を移り替わりながら計算をします。 さて、 の計算が 時間続いたとします。 の様相の列 を考えると、 は、時刻 1 から の間に、少なくと一回は出現しているはずです。 ここで、ある様相から次の様相は一意に定まることに注意すると、結局、 は無限ループに入っていることになります。 従って、 が 時間で計算を終了しない時は、停止しないと判断できることになります。Q.E.D.
次を証明しなさい。
が領域構成可能関数だと仮定する。 また とする。 その時、 どんな領域計算量 の Turing 機械にも計算できない、領域計算量 で計算できる関数 が存在する。
かつ となる はどちらも単調非減少関数としても見つかります。 そのような例を一つ挙げなさい。
次回は計算時間の下限が示されている問題を紹介します。