第 4 回万能 Turing 機械

本日の内容

4-1. 宿題の解答
4-2. Gödel Numbering
4-3. Turing 機械のコードのインタプリタ(万能 Turing 機械)
4-4. 他の計算モデルとの関係
4-5. 宿題
4-6. 次週の予告

4-1. 宿題の解答

カッコ言語の時間計算量は次のように見積もれます。

k テープ Turing 機械の場合

入力を読むテープヘッドは逆戻りせず、一回だけ入力を読むので、 $O (n)$ 時間。

1 テープ Turing 機械の場合

1 テープ Turing 機械では閉じカッコを見つけるとそれに対応するカッコを探すためヘッドが戻り、対応を確認したらもとの閉じカッコの隣へと復帰します。閉じカッコを発見した時、ヘッドが戻り、復帰する動作にかかるヘッドの移動距離は高々 $2 n$ 時間。閉じカッコは高々 $n$ 個あるので、全体の時間計算量は $O (n^{2})$

4-2. Gödel Numbering

今回は Turing 機械のインタプリタを構成します。そのためには、Turing 機械自身を Turing 機械で扱えるデータにしなければなりません。そのために、Gödel Numbering という符号化を行います。

Pairing Function

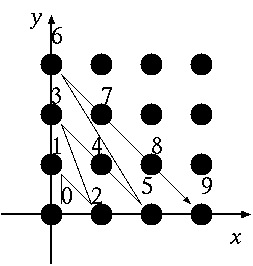
まず、二つの自然数を一つの自然数で表すことを考えます。これは、 $x, y$ 座標面上の格子点を図のように数えていくことにより実現します。

つまり、 $π (00) = 0$ , $π (01) = 1$ , $π (10) = 2$ , $π (02) = 3$ , $π (11) = 4$ , $π (20) = 5$ , … が成り立つような関数 $π$ を求めます。

この数え上げを実現させるには次のように $π$ を計算します。

斜め右下がりの直線上に乗っている $x, y$ は、 $y$ 切片を $k$ と置くと $x + y = k$ が成り立っている。
一本の直線上に乗っている点の数は $k + 1$ 個である。
従って、 $π (0 y)$ の値は $\sum_{k = 0}^{y - 1} k + 1$ になる。
従って、 π は次のように計算する：
$π (x y) = (\sum_{k = 0}^{x + y - 1} k + 1) + x$
$= \frac{(x + y) (x + y + 1)}{2} + x$

演習4-1

$π (34)$ を求めよ。

演習4-2

$π (x y) = z$ のとき、 $π_{l}^{-1} (z) = x, π_{r}^{-1} (z) = y$ と定義する。

$π_{l}^{-1} (25), π_{r}^{-1} (25)$ を求めなさい。
$π_{l}^{-1}, π_{r}^{-1}$ を求めるアルゴリズムを示しなさい。

素因数分解

任意の自然数の列 $(n_{1}, n_{2}, ... n_{k})$ を一つの自然数に埋め込む方法を考えます。これは、効率さえ問われなければ次のようにすることにより実現できます。

素数の列を $p_{1} = 2, p_{2} = 3, ...$ とします。その時、 ${p_{1}}^{n_{1}} \cdot {p_{2}}^{n_{2}} \cdot ... \cdot {p_{k}}^{n_{k}}$ は一つの数を表しますが、素因数分解の一意性から、この数が与えられれば正しく元の数 $(n_{1} n_{2} ... n_{k})$ を復元することができます。

演習4-3

168750 はどのような数列を表しているか？

Turing 機械のコード化

Turing 機械は、次の 5 つの組で定義できます。

状態(ラベル)の有限集合
アルファベット(使用する記号)の有限集合
初期状態(最初のラベル)
終了状態の有限集合(accept するラベルの集合)
δ関数

集合を一つの数にするには、要素を表す文字列を二進数などで表し、それをカンマなどの区切り記号で列挙すれば可能です。但し、状態、アルファベットなど、どんな記号を使うかが本質ではなく単純に数が分かればいい状態だと、集合の要素数のみで事足ります。終了状態の集合だけはすべての要素を列挙しなければならないでしょう。 δ関数は ( 現在の状態, 入力文字₁, 入力文字₂, ..., 入力文字_k, 次の状態, 出力文字₁, 出力文字₂, ..., 出力文字_k, ヘッドの移動₁, ヘッドの移動₂, ..., ヘッドの移動_k ) を必要な分だけ繰り返すことで表現できます。

結局、Turing 機械の構成は多くの数の組で表現できることが分かります。そのため、それを前節までで説明した手法により、一つの自然数を Turing 機械の定義と解釈することができます。

また、素因数分解を使用したコード化において、あらゆる数列が一つの数になります。そのため、自然数によって Turing 機械のコードを全て数え上げることができます。

4-3. Turing 機械のコードのインタプリタ(万能 Turing 機械)

Church の提唱を使えば、Turing 機械のコードを解釈する Turing 機械が存在することは言えます。しかし、計算量や Turing 機械のテープ数による能力の違いを議論するため、ここでは Turing 機械の構成の概略を説明します。

万能 Turing 機械とは Turing 機械のコードと、本来与えるべき入力の対から、そのコードの指す Turing 機械に入力を与えたときの出力を出力する Turing 機械を指します。

テープが十分に多い万能 Turing 機械

ここでは、与えられた Turing 機械のコードが仮定しているテープ数に比べて、十分にテープ数を持つ Turing 機械により、与えられたコードのδ関数を 1 step 実行する方法を説明します。

与えられたコードが k 本テープを使用する Turing 機械を表しているとします。その時、まず、 k 本のテープをそのシミュレートする Turing 機械が使用するテープとしてそのまま割り当てます。次に、シミュレートの作業用に、与えられたコードを記憶するために 1 本、シミュレートしているTuring 機械の状態を記憶するために 1 本、シミュレートしている Turing 機械のテープヘッドの位置を記憶するテープを k 本用意します。

さて、 Turing 機械の 1 step のシミュレーションの手順を示します。まず、現在の状態と、テープの位置の記号から、それに適合するδ関数の値を読みだします。これにはコードを解析する必要があります。コードを解析するには、素数を生成して素因数分解を行う必要があります。まず、一本のテープに素数列を生成します。これは素朴にエラトステネスのフルイを使用します。 Turing 機械のコードの長さを $d$ とすると、必要な素数の長さも $d$ ですので、必要な素数の最大値は高々 $2^{d}$ までになります。一方、割算 $x \div y$ を実現するには、 $x$ を始めに記憶しておき、 $y$ を桁をずらしながら引き算が可能かどうかを調べていきます。これは、結果を入れるテープを含め 3 本のテープを使い、 $O (log x log y)$ 時間で計算できます。よって、コードから一つのδ関数の割り当てを取り出すためには、素数を順に生成していき、各素数で割れるだけ割ることで取り出すことができます。素数の生成に $O (2^{d})$ 時間かかるので、適合するδ関数の値を読み出すのに、 $c$ を定数とすると、 $O (2^{c d})$ 程度の時間がかかります。また、テープは数本(5〜6本)余分に使用します。そして、読み出したδ関数の値に従い、各テープに記号を書き、移動させます。結局、シミュレーションに使用するテープは数本で、かかる時間は $O (2^{c d})$ 程度になります。但し、 $d$ があらかじめ与えられた定数だとすると、もともとの Turing 機械の定数倍の時間だけかかると言えます。

1 テープ Turing 機械でのシミュレーション

前節のシミュレーションでは、与えられた Turing 機械のコードに対して、さらにテープを追加してシミュレーションしました。ここでは一つ Turing 機械を固定してあらゆる Turing 機械をシミュレートすることを考えます。そのため、与えられた時間計算量 $T (n)$ の k テープ Turing 機械を $O ({T (n)}^{2})$ 時間でシミュレートする 1 テープ Turing 機械を構成します。

1 テープ Turing 機械で k テープ Turing 機械を 1 step シミュレーションするにはテープを次のように使います。

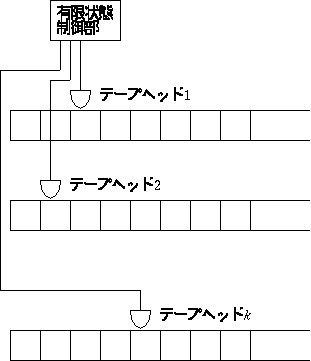
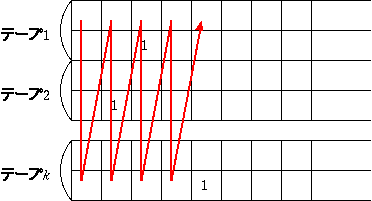
各テープの内容は $2 k$ ます毎に書かれます。各テープは 2 マスを対にし、一マスはテープの内容を、もう一マスはテープヘッドがなければ 0 、あれば 1 を記入します。そして、シミュレーションでは毎回各テープのヘッドの位置を読み込みます。各テープのヘッドの記号を覚えておくため、 $k$ マスのテープ領域はあらかじめ用意しておきます。そしてδ関数を計算します。 δ関数により得られたテープへの書き込み文字やテープヘッドの移動に関しては、各テープのテープヘッドの位置に目的の記号を書いてヘッドを動かすことをシミュレートします。一回に一つのテープだけを対象にすることで、書き込む記号の種類は有限個になります。したがって、テープヘッドを検索してヘッド位置に記号を書き、ヘッドを移動する処理を行うために、書き込む記号ヘッドの移動方向ごとに異なるラベルを使用すれば、あらたなテープ上の記憶は必要ありません。結局、 1 step のシミュレーションで必要なのは、各テープヘッドが読み書きする記号を保存する k マスの領域と、ヘッドの検索時間と書き込む時間になります。もともとの Turing 機械の時間計算量が $T (n)$ であれば、その時間内に使用できるテープのマスの最大値はやはり $T (n)$ ですので、一回の検索にかかる時間は高々 $O (T (n))$ 時間でできます。これを 1 step のシミュレーションで定数回行います。最終的にこのシミュレーションは $T (n)$ 回行うので、時間計算量は $O ({T (n)}^{2})$ になります。

なお、最初の状態では入力の値が一マス毎に書かれている状態なので、シミュレーションの準備をしなければなりません。しかし、これは、テープの最初に $k$ マスの領域をとり、その後、 $2 k$ マス毎に入力の値をコピーします。これにかかる時間は入力の長さ $n$ に比例します。

注釈

2 テープ Turing 機械だと $O (T (n) log T (n))$ 時間でシミュレートできることが知られています。

実際のシミュレートの仕方は笠井琢美「コンピュータサイエンス大学講座 17 -- 計算量の理論」近代科学社(1987) に詳しく載っています。

基本的なアイディアは以下の通りです。

k テープ Turing 機械としてテープの両方が無限にあるようなものを考える。初期のテープヘッドの位置を原点と呼ぶことにする。
シミュレーションでは適当な区切りごとに、k 個のテープヘッドが全て原点に戻るようにシミュレートする
そのため、テープヘッドの位置を覚えるのではなく、テープの内容を移動させて、本来テープヘッドがある位置が原点になるように、テープの内容をコピーする。
t ステップシミュレートすると、ヘッドの移動距離は高々 t マスになる。そのため、 t 時間まとめてシミュレートした後、コピーしなければならないテープのマス目は t マス。
最初は 1 ステップシミュレートとする。その時、テープヘッドが動作する範囲を考えると± 1 マスなので、原点とその両隣のマスを一括して書き換えるようにする。
次に、シミュレートの時間を 2 ステップ、 4 ステップと倍々に増やすことを考える。再帰的に考えると、 i 時間のシミュレートが可能な時、それを二度行うことで 2i 時間のシミュレートを実現したい。
そのため、テープをコピーする際に、新たな領域をその都度生成しないようにしたい。また、テープを 1, 2, 4,... マスごとのブロックに分割する。
2^i ステップのシミュレーションでテープヘッドは i ブロックしか移動しない。そのため、移動に必要なコピーをしてもひとブロックを使いきるだけで済む。そこで、 1 本のテープにつき、3 マスごとにテープを使うようにし、各ブロックとも 3 個ずつ領域があるようにする。 j ブロック目が 3 領域とも埋まっているなら、二個のブロックをまとめて隣のブロックにつなげてコピーする。またブロックが空なら、隣のブロックを2分割して、二つの領域に分けて格納する。

このようにすると、 $2^{i}$ ステップのシミュレーションに $r (i)$ 時間かかるのであれば、 $2^{i + 1}$ ステップのシミュレーションには $r (i + 1)$ 時間かかることになる。

さて、ここで、十分大きな定数 c を用いて $r (i)$ を表すと次のようになる。

r (0) \leq c

r (i + 1) \leq 2 r (i) + c 2^{i}

これは次のように計算できる。まず、右の項に注目して、 i を減らして 2 倍すると次が得られる。

2 r (i) \leq 4 r (i - 1) + c 2^{i}

これを片々引き算すると次が得られる。

r (i + 1) - 2 r (i) = 2 (r (i) - 2 r (i - 1))

= 2^{i - 1} (r (1) - 2 r (0)) = 2^{i - 1} (4 c - 2 c) = c 2^{i}

ここで以下の和を考えると、 $r (i)$ が求まります。

\begin{matrix} r (i) & - & 2 r (i - 1) & = & c 2^{i} \\ 2 (r (i - 1) & - & 2 r (i - 2)) & = & c 2^{i} \\ ... \\ +) & 2^{i - 1} (r (1) & - & 2 r (0)) & = & c 2^{i} \\ ------------------------------------------------------------------------- \\ r (i) & - & 2^{i} r (0) & = & i c 2^{i} \end{matrix}

したがって以下を得ることができます。

r (i) = (i + 1) c 2^{i}

ここで上記の議論を 1 テープと同様にテープを k マスに拡張して考えます。但し、帰納的にシミュレートするため、スタックが必要となるので、上記を実現するためにもう一本テープが必要です。そのため、 2 本テープが必要です。また、 $T (n)$ ステップで計算が終わるような Turing 機械をシミュレートするとき、 $i$ として高々 $log T (n)$ までシミュレートすれば計算が終ります。したがって、その時の実行時間は $O (T (n) log T (n))$ になります。

補足

$T (n)$ 時間 Turing 機械を定数本のテープを持つ Turing 機械でシミュレーションするとき、シミュレーションの時間が $Ω (T (n) log T (n))$ であるかどうかは重要な未解決問題です。

演習4-4

1 テープ Turing 機械のシミュレーションの仕方において、テープのマス目の使用量を見積もりなさい。つまり、領域計算量 S(n) の Turing 機械において、 1 テープ Turing 機械ではどの程度のテープのマス目が必要か？

4-4. 他の計算モデルとの関係

一般のプログラムにおいて、配列変数を除外して考えると、通常の変数に対してテープ一本を割り当てるような k テープ Turing 機械に対応づけることができます。これは自明ではありませんが、特定の CPU の 1 step の動作を、レジスタの本数だけテープを用意した k テープ Turing 機械で定数ステップで動作させられるように作ることができます。 C 言語のプログラムもそれぞれの命令が定数ステップの機械語に変換され、それぞれの命令において、データの長さに応じたステップ数がかかると仮定するとします。その時、前回の C 言語のプログラムのステップ数の計算のうち、データの長さに比例したような見積りを行うことを考えます。 T(n) ステップで動作するような C 言語のプログラムは結局 2 テープ Turing 機械で O(T(n)log T(n)) 時間でシミュレートできることになります。

4-5. 宿題

万能 Turing 機械のコードの長さ $d$ に対して、シミュレーションの時間計算量が $d$ の多項式に比例する(多項式時間)ようにするにはどうすれば良いか?

4-6. 次週の予告

計算不能な問題を取り上げます。

坂本直志 <sakamoto@c.dendai.ac.jp>
東京電機大学工学部情報通信工学科

第 4 回 万能 Turing 機械