このドキュメントは http://edu.net.c.dendai.ac.jp/ 上で公開されています。
並列計算も分散アルゴリズムも、複数のプロセッサが協調して動作することは 同じです。 並列計算とは、問題に対してプロセッサ群によるネットワークを構築し、問題 を解決するための行う計算を指します。 一方、分散アルゴリズムは既に存在するネットワーク上のプロセッサが協調し て行う計算で、計算の目標はそのネットワーク自体に存在する問題の解決です。 分散アルゴリズムの例として、複数のプロセスによるデータベースアクセスの デッドロックの解消や、ダイクストラのダイニングフィロソファー問題などが 知られています。 さらに、これだけではなく、インターネットの管理などには分散アルゴリズム が積極的に使用されています。

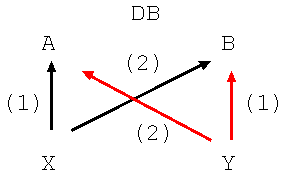
WWW などでは多くのアクセスに対して並列的に処理が行なわれます。 また、 WWW での処理においてしばしばデータベースが使用されています。 例えば、ショッピングモールサイトなどで、あるユーザ X が A の条件を基に B を書き換える操作を要求するとします。 一方、別のユーザが B の条件を基に A を書き換えるとします。 この時、この X と Y が同時に発生するとデッドロックが発生します。 つまり X が A を確保した後、 B を書き換える前に、 Y が B を確保し、 A を書き換えようとしている状況が発生します。
デッドロックを実際にどう解決するかはデータベースの問題ですが、各 X や Y がデッドロック状態に気づくためには、それぞれの操作を行なうプログラム 内で処理する必要があります。 つまり同一の Web アプリケーションプログラムを動かす複数のプロセスが 互いにデッドロックを検知する必要があります。 これは相互に要求している資源の関係をプロセス同士が通信を行ないながら取 得し、要求の関係からデッドロックを検知します。
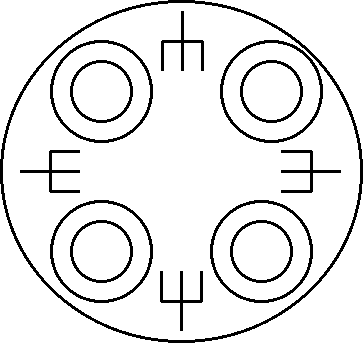
ダイニングフィロソファー(哲学者の食卓)問題とは丸テーブルに哲学者が座っ て食事をする際に生じる抽象的な問題です。 食卓には皿、フォーク、皿、フォークと順に丸く配置されているとします。 その際、哲学者は右または左のフォークを取って食事を始めるとします。 各哲学者はどのようにして右または左を決定するのでしょうか? 誰か一人がどちらかのフォークを取れば隣の哲学者はそれと同じ側のフォーク を取ることで全員がフォークを手にすることができます。 しかし、その一人をどのようにして決めるのでしょうか? このようにダイニングフィロソファー問題は相互にどのようにしてフォークを 取るかを哲学者が思考し、いつまでも食事を始められない状況をどのように打 開するかと言う問題です。
インターネットの経路制御には経路表が使われます。 経路表にはネットワークアドレス、転送先アドレス、メトリック(距離)が記 述されています。 この経路表をネットワーク上で相互に通信し合いながら計算するプログラムを ルーティングプロトコルと呼びます。
RIP というルーティングプロトコルは距離ベクトル型のプロトコルです。 これは各RIPの動いているルータは以下のようなプロトコルを実行します。
このようにインターネットではルータが相互に同一のプログラムを実行してネッ トワークの制御を行なっています。
分散アルゴリズムはネットワークを固定しません。 そのため、条件を満たす任意のネットワーク上で動作できるよう、各プロセッ サでは同一のプログラムを動かします。 但し、多くの分散アルゴリズムでは各プロセッサにはユニークに番号が振られ ていることが仮定されています。 一方、この番号を振ること自体も分散アルゴリズムの問題になり得ります。
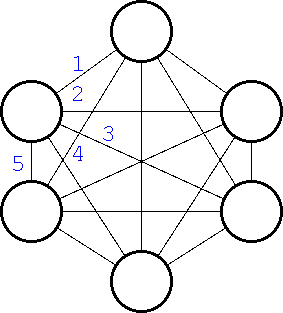
この節では分散アルゴリズムの例を考えるため、番号を振る分散アルゴリズム について考えます。 問題の前提条件として各プロセッサには番号が振られていないとします。 また、全頂点は相互に一対一に接続され、互いに通信ができます(完全グラフ)。 ここで全プロセッサ数を N とすると、各頂点の持つ通信線は(N-1)本あるため、 各プロセッサは全プロセッサ数 N を知っており、また通信線には 1 から N-1 まで番号が振られていて通信相手を全て区別することが可能です。
この状態で全頂点に同じプログラムを与えプログラムが終了したときに各プロ セッサはそれぞれ異なる番号を所持しているようにできるかがこの問題です。
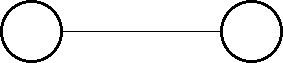
始めに隣接している二つのプロセッサに同じプログラムを走らせて、どちらか が 0, どちらかが 1 を出力するプログラムを考えます。 これを行なうのにじゃんけんを考えます。 じゃんけんではプロセッサは 0,1,2 のどれかをランダムに選びます。 そして、二つのプロセッサ同士で選んだ値を比較します。 比較は 0<1<2<0 の順番とし、小さい方が 0, 大きい方が 1 を出力 します。
さて、この場合、勝負が着くまで繰り返すとして、繰り返し回数の平均値を求 めましょう。
この時、決着が着く平均繰り返し回数 E は次で得られます。
この無限和に対して、 n 項目までの和 Enを考えます。
これに 1/3 を掛けると次のようになります。
これを辺々で引き算すると次が得られます。
このn の極限をとると E が次のように求まります。
つまり、平均 1.5 回の繰り返しで決着が着くことがわかります。
次に二人ではなく、 n 人でジャンケンで順番を決めることを考えます。 全員でジャンケンをする時、あいこになる確率は次で求められます。
よりあいこの確率は n が大きくなると 1 に近付いていきます。 すると決着の着く回数も n が大きくなるにつれ大きくなっていきます。 これはあまり効率のよい方法ではありません。
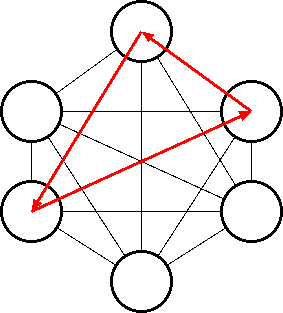
次に全員と一回ずつ二人だけのジャンケンの総当たり戦をし、集計することを 考えます。 二人だけのジャンケンだと勝負が着くまで平均 3/2 回、 n 人だと 3n/2 回で収束 します。 但し、A,B,C の三人で行う場合を考えると、 A は B に勝ち、 B は C に勝ち、 C は A に勝ちとサイクルができてしまうことが考えられます。 この場合、全体で勝負が着きません。 勝敗の着き方は 23 で 8 通りありますが、この中でサイクルは右 まわりと左まわりの 2 通りありますので、 1/4 の確率で勝負が着きません。 n 人でサイクルが発生する確率は以下のようになります。
これでは n が大きくなると勝負がつく可能性が 0 に収束してしまいます。
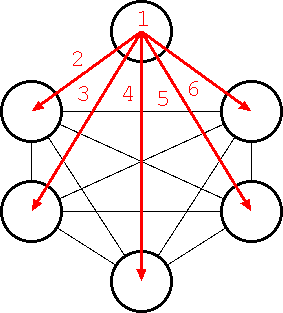
ここまで分散的に番号を振ることを考えてました。 しかし、このような問題の場合、逆にサーバ/クライアントモデルを考えると 容易に番号を振ることができます。 つまりあるプロセッサだけがサーバとして機能していれば、このサーバが接続 先に(通信線に付けられた)番号を送ることで全プロセッサに番号を振ることが できます。 そこで、分散アルゴリズムとしてサーバを一台決定することを考えましょう。 二つのプロセッサ毎にジャンケンで勝敗を決めていき、一回でも負けたプロセッ サはクライアントになることにします。 これはトーナメント戦になるので、全体で n-1 戦のジャンケンをするとサー バのプロセッサが一つ決まります。
Apple社の Macintosh はネットワークに接続すると特にアドレスの設定をしな くても相互に通信が可能です。 これは以下のような手順(プロトコル)によりアドレスを自動的に付けているか らです。
Apple Talk というプロトコルはシリアル、あるいは Ethernet 上で使用され ますが、どちらも何十台も同一セグメントに Macintosh を配置しませんので、 これは十分機能します。 但し、このプロトコルからわかるように 126 台以上 Macintosh が存在するこ とはできません。
J. Bar-Ilan and D. Zernik "Random Leaders and Random Spanning Trees", "Distributed Algorithms", Lecture Note in Computer Science. Vol. 392.(1989) pp. 1-12
この論文に載っているアルゴリズムは順に番号を振るものではなく、バラバラ の数を振るものです。 これは Apple Talk と同様、乱数を単に選ぶだけです。 但し、全頂点数 n に対して、乱数を選ぶ範囲を 1 から n3 までとします。 この時、うまくいく確率を次のように見積もります。
これに対して以下の公式を適用します。
以下のように変形することで成功確率を見積もります。
これは n が大きくなると 1 に近づきます。
以上、いろいろな番号を振る方法を考えてきましたが、全て何らかの前提条件 を必要としていました。 これに関してまとめます。
通常の分散アルゴリズムでは個別の識別子や頂点数などを前提とするのが普通 です。 今回のように個別の識別子を求めるには、それらを前提にできません。各プロ セッサが識別子を持たないネットワークを匿名ネットワーク (Anonymous Network)と言います。 なお、ここでの議論により全くの匿名ネットワークでは番号を振ることができ ないことがわかっています。 そこで、何らかの入力を与えて番号を得ることを考えます。
ネットワークに対する入力の与え方により研究の切口が変わってきます。 次回はこの研究の先がけとなった Angluin の研究を紹介します。
D. Angluin "Local and Global Properties in Networks of Processors" 12th Symposium on Theory of Computer Science.(1980)
問題: ネットワーク(分散システム)が機能するためには、各プロセッサは自分 のID、他のID、ネットワークの構造などどのような情報をどれくらい知らなく てはならないのだろうか? そのためのアプローチとして、まず、各プロセッサにほとんど何も情報のない 状態で仕事をさせます。 この何も情報の無い状態はどのようにして与えるかというと、同じ次数のプロ セッサは同じプログラムを与えることにします。 そして、どのようなグラフにおいて、目的の仕事(生成木を作る等)ができるか 考えます。
計算ができる、できないを議論するため、計算を厳密に定義する必要がありま す。 そのため、ネットワークをグラフとチューリング機械のような物を使って表現 します。
正整数 d に対して とします。 アルファベット A とは記号を表現するものの集合で、有限で少なくとも二つの要 素を持つものとします。
次数 のプロセッサとは の二つ組で表されます。
ここで M(q,i) は (a,b,q') という組の集合に対応づけられます。 これが意味するのは、状態 q のプロセッサがポート i のプロセッ サとメッセージ a と b を交換して、新たな状態 q' に遷移することです。
プロセッサが有限状態とは Q が有限集合であることです。
pd を次数 d のプロセッサとするとき、プロセッサの列とは (p1, p2, ... ) という無限列を示す。
ネットワークをグラフ、ポートナンバリング、プロセッサの列の三つ組み (G∈G, {fv}, (p1, p2, ...)) で定義する。
ネットワークの configuration c(v) とは G の頂点 v から pdeg(v) の状態を対応づける関数とする。
c1, c2 が configuration の時、 c1 が 1 step で c2 に遷移する ( ) とは次の二つの条件を満たすことを言う。
つまり、 configuration が 1 step 推移するとは、頂点 u, v がメッセージ a, b を交換して状態を遷移する一方、他のプロセッサはそのままであること を言います。 なお、この定義では遷移の過程で必ず一つだけのメッセージが送られているこ とを保証することになります。 これを利用すると他の分散システムの定義に比べ特殊なことができます(後述)。
c0から遷移可能な configuration は複数あり、また遷移した configuration からもまた複数の configuration に遷移が可能である。 繰り返し遷移可能な configuration を並べると、c0 を根とした 有向木になる(但し、木の頂点のラベルを configuration とした時、同一のラ ベルの存在を許す)。 また、 の反射推移閉包を で表します。 は c0 の木の中に c が存在すること、つまり、 という関係を意味します。
c0 からの計算とは c0 から到達可能な c0 の木の極大の path を示します。 これは根から始まり、最後の configuration からの遷移が無い場合だけ有限 になります。
グラフ H,G ∈ G と p:V(H)→V(G) に対して、 H が p による G の covering であるとは、 H に含まれる各頂点 v に対し て、p の定義域を NH(v) に限定すると NG(p(v)) に 対して一対一対応になることを意味します。
例えば H として頂点 6 のリング状グラフ、 G として頂点 3 のリング状グラ フとします。 それぞれ、頂点のラベルが {1,2,3,4,5,6} と {a,b,c} とし、p は p(1)=a, p(2)=b, p(3)=c, p(4)=a, p(5)=b, p(6)=c とします。 すると、頂点 1 に対しては NH(1)={2,6}, NG(p(1))={b,c} で、 p(2)=b, p(6)=c は一対一になります。
また、単に H が G の covering であるとは、このような条件を満たす p が 存在することを意味します。 H と G が有限の共通 covering を持つとは、 H と G の covering となる K∈G が存在することを言います。 H が G の covering で、 H と G が同型でない時、 H は G の proper covering と言います。
例えば 4 頂点のリング状グラフと 6 頂点のリング状グラフに対して、 12 頂 点のリング状グラフは有限の共通 covering となります。
プロセッサの列 (p1, p2, ...) の各プロセッサが zd, cd という異なる状態を持っている時、 c0 が uniform initial configuration であるとは、 c0(v)=zdeg(v) であること、 c0 が centered configuration であるとは、 ただ一つの頂点 v にとって、c0(v)=cdeg(v) であること、 c0 が forbidden configuration であるとは、 二つの異なる頂点 v,w に対して、c0(v)=cdeg(v), c0(w)=cdeg(w) であることです。
(p1, p2, ...) が G で deterministically establishes a center とは c0 からの全ての計算にお いて centered configuration を含み、また forbidden configuration を含まないこと。 また、(p1, p2, ...) が G で nondeterministically establishes a center とは c0 からの ある計算が centered configuration を含み、 また全ての計算において forbidden configuration を含まないこと。
全ての完全グラフに対して deterministically establishes a center となる プロセッサの列が存在する
計算モデルにおいて、メッセージが常に一つだけしか流れないことが保証され ているため、対向の頂点同士において同時にメッセージを出すことは無く、必 ずどちらか一方がメッセージを出すことが保証される。 これを利用して後にメッセージを出す方は center の状態に入らないようにす れば、最終的に一つの頂点だけが center の状態に入ることができる。
なお、現実的な分散システムにおいて、常に一つだけメッセージが流れること は保証されない。 従って、この定理は計算モデルに依存した結果であると言える。
4 頂点のリング状ネットワークを S4 で表す。 この時、 S4 で determinstically established a center ができ るプロセッサは存在しない。
頂点の configuration が偶数時間に A,B,A,B と交互に同じ状態になっている と仮定します。これは一番最初は A=B ですが条件を満たします。 このような前提に対して、次の偶数時間に同じ条件が成り立つような遷移があ ることを示す。
これは A と B の組を頂点と考えると、同じ状態なら同じ通信を行う configuration が存在するという論法。 一方の A が B にメッセージを送ると、次の step で 一度に一つのメッセージしか存在しないことを利用して単独のプロセッサだと 相互に異なる状態に入れるが、二つ以上のプロセッサの組だと組の数分のステッ プで通常の同期モデルにおける同時送信と同じ現象が生じる。
非決定性(nondeterministic)は実用上あまり意味が無いので、定理 4.3, 4.5, 4.6 は省略。
G に含まれる任意の木に対して deterministically establishes a center できるプロセッサの列が存在する。