
変数に null が入っている場合
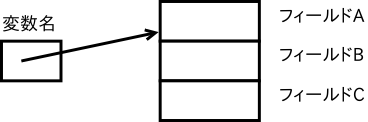
変数にオブジェクトの位置情報(参照)が入っている場合
主に変数とオブジェクトの区別が付いていないこと、また、 null がオブジェ クトであるとの誤解をしていることが原因と思われます。
| 基本型変数 | オブジェクト型変数 | オブジェクト | |
|---|---|---|---|
| 名前 | 変数名 | 変数名 | 付かない |
| 中に含まれるもの | 具体的な値 | オブジェクトの位置情報(参照)がひとつだけ、または null | 0個以上の変数(フィールド) |
| 作り方 | 基本型名と変数名を並べる | クラス名と変数名を並べる | new 演算子に よるコンストラクタの呼び出し |


特に、 Java ではオブジェクトはオブジェクトや変数を指すことができませんし、変数もオブジェクトは指せませすが、変数を指すことができません。 変数が何かから指されていたら完全に誤りです。
TDUMapEntry は java.util.AbstractMap.SimpleEntry を継承しています。 TDUMapEntry 自体は left と right のフィールドを定義していますが、さら に、親クラスで取り扱う値があります。 これらを合計すると、 TDUMapEntry オブジェクトにいくつフィールドが含ま れるかが分かるはずです。
例えば、次のプログラムで下記の説明が無意味なのはわかるはず。
private static int combination(int n, int m){
if(n==0 || n==m) return 1;
return combination(n-1,m-1)+combination(n-1,m);
}
nが 0 か m と等しいときは 1 を返している。そうでなければ combination(n-1,m-1)+combination(n-1,m) を再帰的に返している。
再帰の説明をするには、なぜ再帰を使うのか、使えるのかを説明しなければ意 味をなしません。 上記の場合だと、組み合わせの数の性質として、一つの要素を選ぶような説明 が必須です。
課題2のプログラムの説明において、なぜ再帰になるかに関しては、木の一部 分はやっぱり木になるという性質を既知のものとして説明して下さい。
課題2-1の Ex21 は配列を表示するプログラムではありません。 java.util.Set を実装したクラスのオブジェクトを表示するプログラムです。
以下では、レポートに書いたら不合格になるような図や説明の例を挙げます。
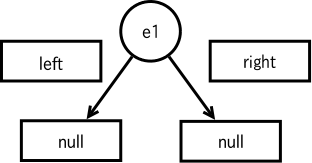
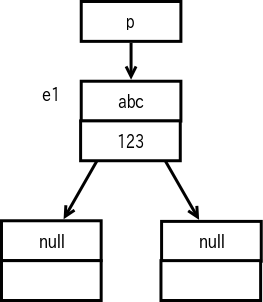
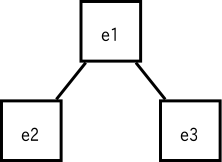
下記のテストプログラムは値の順番が狂うのでお蔵入りしていましたが、課題 2-1 の問題を作り替えている人がいますので、公開することにします。 順番は変わってしまいますが、同じ数要素が出力されれば合格です。
import java.util.Set;
import java.util.HashSet;
import java.util.Arrays;
import tdu.*;
class Ex212 {
private static <E> void print(Set<E> s){
for(E e : s){
System.out.println(e);
}
System.out.println(s);
}
public static void main(String[] arg){
Integer[] array = {9,1,2,8,3,4,5,7,6};
array[2]=null;
TDUSet<Integer> set1 = new TDUSet<Integer>(array);
HashSet<Integer> set2 = new HashSet<Integer>(Arrays.asList(array));
print(set1);
print(set2);
}
}
なお、java.util.Iterator の next では要素の範囲を越えたら
NoSuchElementException 例外を発生しなければならないようですが、見落と
していました。
本来なら next の一行目に
if(!hasNext()) throw new NoSuchElementExeption();
を加えなければなりませんが、無くても今回は不合格の理由にしません。
traverse の説明をする際、プログラムが実行される際の Java の動きを意識 してプログラム自体の説明をしてしまうとうまく説明できません。 再帰のプログラムを説明する場合、再帰関数の仕様のみを意識し、それを適用 すると当然のように仕様通りの動作をするように説明します。
再帰処理というのは非常に複雑です。例えば、次のようなプログラムがどのよ うに動作するかを意識するのはとても難しいです。
class Rei {
private static int m(int n){
if(n>100) return n-10;
return m(m(n+11));
}
public static void main(String[] arg){
for(int i=1; i<200; i++){
System.out.println(""+i+": "+m(i));
}
}
}
再帰というテクニックは非常に強力な計算能力を持っています。 理論的に知りたい人は「帰納的関数」や「原始帰納的関数」などのキーワード を調べると良いでしょう。