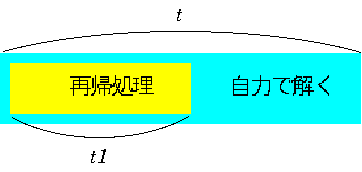
 ある問題を解く際に、その問題を同じ性質を持つ小さい部分に分解できるとし
ます。
すると、その問題を解く関数 solve は再帰処理を使うと次のように書くこと
ができます。
ある問題を解く際に、その問題を同じ性質を持つ小さい部分に分解できるとし
ます。
すると、その問題を解く関数 solve は再帰処理を使うと次のように書くこと
ができます。
このドキュメントは http://edu.net.c.dendai.ac.jp/ 上で公開されています。
自分の先祖を考えると、これは、おとうさん、おかあさん、おとうさんのおと うさん、おとうさんのおかあさん……と永遠に記述しなければならなくなりま すが、これを「おとうさん、おかあさんと、おとうさんの先祖とお母さんの先 祖」と言う風に、先祖を規定するのに先祖という言葉を使って規定すると形の上 では短い表現で記述できます。 これを帰納的定義といいます。 なお、一見循環論法に見えますが、「先祖とは先祖です」という文とは違いま す。 「先祖」を「おとうさんとおかあさんとおとうさんの先祖とおかあさんの先祖」 とすると、さらに「おとうさんとおかあさんとおとうさんの「おとうさんとお かあさんとおとうさんの先祖とおかあさんの先祖」とおかあさんの先祖」と置 き換えることができます。 この置き換えを繰り返すことで、最初に述べた「おとうさん、おかあさん、お とうさんのおとうさん、おとうさんのおかあさん……」と同じことが表現でき ることがわかります。 帰納的定義はこのように短い記述で無限の構造を表現できるという性質があり ます。
関数の定義で自分自身の関数を呼び出すことを再帰と言います。 再帰も帰納的定義になります。 Java 言語は再帰が可能なため、関数定義で帰納的定義を使用することができます。 これを使うと、短い記述で複雑な問題を解くことができます。
 ある問題を解く際に、その問題を同じ性質を持つ小さい部分に分解できるとし
ます。
すると、その問題を解く関数 solve は再帰処理を使うと次のように書くこと
ができます。
ある問題を解く際に、その問題を同じ性質を持つ小さい部分に分解できるとし
ます。
すると、その問題を解く関数 solve は再帰処理を使うと次のように書くこと
ができます。
public staitc int solve(解くべき問題 t){
if(t がもう分解できない){
t を処理;
return t の答え;
}
t1 = t と同じ性質を持つ小さい部分;
ans1 = solve(t1); /* 再帰 */
分解した残りと ans1 によりtの答を計算;
return t の答え;
}
階乗 n!=n*(n-1)*...*2*1 は n!=n*(n-1)! と右辺にも階乗を含む構造に分解 できます。 一方 0!=1 となります。 従って、プログラムは次のようになります。
public static long kaijo(int n){
if(n==0){
return 1;
}
return n*kaijo(n-1);
}
フィボナッチ数列とは、手前の数と、その手前の数の和を次々と求めてできる 数列です。
a0=1, a1=1 とすると、n 番目(n≧ 2)は an= an-1+ an-2 と書けます。 この時の n 番目の値を求める関数は素朴な書き方をすると次のようになり ます。
public static long fibo(int n){
if(n==0) return 1;
if(n==1) return 1;
return fibo(n-1)+fibo(n-2);
}
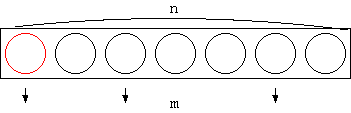
組合せの数 nCm の求め方を考えます。 これは n 個の中から m 個を取り出す取り出し方は何通りあるかということで す。 ここで、n 個のものの中から一つのものに注目します。
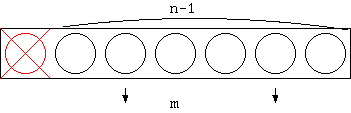
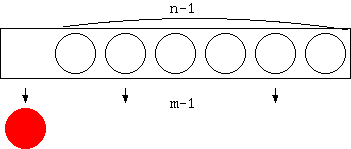
従って、 nCm = n-1Cm + n-1Cm-1 が得られます。 なお、n 個のものから0 個を取る取り方や、 n 個全部を取り出す取り方はと もに 1 通りしかありません。つまり nC0 = nCn = 1 です。
ハノイの塔とは次のようなパズルです。 大きさが一回りずつ違う円盤を大きい順に下から並べます。 そして、次のルールでその円盤の山を移動させます。
以下に 3 枚での例を示します。
| a | b | c | ||
|---|---|---|---|---|
| 1 |
= == === --a-- |
--b-- |
--c-- |
|
| 2 |
== === --a-- |
= --b-- |
--c-- |
move 1 from a to b |
| 3 |
=== --a-- |
= --b-- |
== --c-- |
move 2 from a to c |
| 4 |
=== --a-- |
--b-- |
= == --c-- |
move 1 from b to c |
| 5 |
--a-- |
=== --b-- |
= == --c-- |
move 3 from a to b |
| 6 |
= --a-- |
=== --b-- |
== --c-- |
move 1 from c to a |
| 7 |
= --a-- |
== === --b-- |
--c-- |
move 2 from c to b |
| 8 |
--a-- |
= == === --b-- |
--c-- |
move 1 from a to b |
この解法を再帰的に考えます。 もし、hanoi(n-1,"a","b","c") が n-1 枚の円盤を a から b へ移動する解法 を出力するとします(c はもう一つの領域)。 すると、 n 枚の円盤を a から b へ移動する解法は次のように考えられます。
このようにすると hanoi(n,"a","b","c") の解法を出力します。
class Rei {
private static void move(int n, String x, String y){
System.out.println("move "+n+" from "+x+" to "+y);
}
public static void hanoi(int n, String x, String y, String z){
if(n==1){
move(1,x,y);
return;
}
hanoi(n-1,x,z,y);
move(n,x,y);
hanoi(n-1,z,y,x);
}
public static void main(String[] arg){
hanoi(Integer.parseInt(arg[0]),"a","b","c");
}
}
プログラムで扱うデータ構造としてグラフを取り上げます。 グラフとは頂点とそれを結ぶ辺からなるものです。
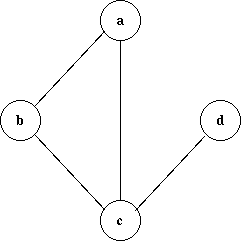
頂点は vertex、 節、 node などの呼び方があります、辺は edge、枝、 branch とも言います。 辺に向きがないグラフを無向グラフ、 辺に向きがあるグラフを有向グラフと言います。
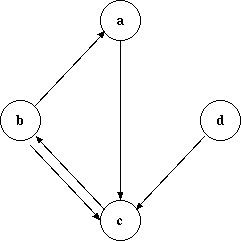
互いに接続している頂点の列を道(path)と言います。 無向グラフにおいて、全ての頂点の組合せについて道がある場合、そのグラフ は連結であると言います。
頂点に接続している辺の数をその頂点の次数、degree 、arityと言います。 有向グラフにおいては出る辺の数を出次数、out degree、入る辺の数を入次数、in degreeと言 います。
グラフには様々な形があり、それについて名前が付けられています。 無向グラフにおいて、木とは、ループのない連結グラフのことを言います。 次数が 1 の頂点を葉、leafと言います。
根付有向木とは、次の条件を満たす有向グラフのことです。
根付有向木で接続している二つの頂点に対して、辺が出る頂点を親 、辺が入る頂点を子と言います。 出次数が 0 (入次数が 1)の頂点を葉と言います。 根付有向木において、出る辺の数が高々 2 本の木を二分木、 二進木、binary tree と言います。
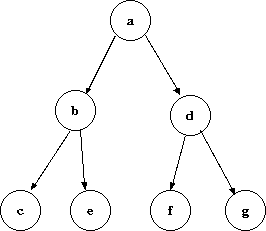
ここでさらに左側の枝には必ず葉が接続する二分木を考えると次のような構造になり ます。 これを線形リストと呼びます。
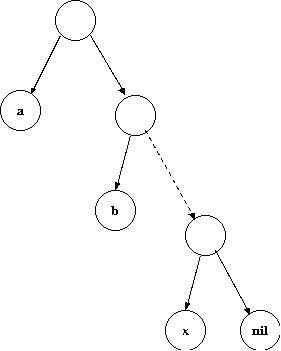
すべての頂点の次数が 2 の連結グラフは リング になります。
また、すべての頂点間に辺がある無向グラフを完全グラフと言い ます。
頂点が二つのグループに分割でき、同じグループ同士には辺がないグラフを 二部グラフと言います。 特に、異なるグループのすべての頂点の組み合わせに辺がある無向二部グラフ を完全二部グラフと言います。
ここで、話が少しそれますが、 Java におけるデータの入力方法をまとめます。
なお、数値入力と言っても、実際にコンピュータは「入力」が「数値」だと直接認識するわけではありません。 仮に「123」のような数値を取得するためには、まず文字である"1" と "2" と "3" を入手し、それらを結合して "123" という文字列を得、それを数を表 す文字列として解釈して最終的に数値にします。
Java での標準入力である java.lang.System.in は java.io.InputStream のイ ンスタンスです。 入力されるデータは基本的には byte の集まりです。したがって、もっとも基 本的な仕組である、 この java.io.InputStream の read メソッドは byte 単位になります。 これを、まず、文字として扱うために java.io.Reader 型に変換します。 但し、java.io.Reader は抽象クラスでインスタンス化できません。 InputStream 型であれば Reader のサブクラスである InputStreamReader を 使用します。 変換するには、InputStreamReader のコンストラクタに InputStream のイン スタンスを指定します。 さらに、文字に変換するため、コンストラクタに文字コードを指定することも できます。
import java.io.*;
...
Reader isr = new InputStreamReader(System.in);
Reader isr = new InputStreamReader(System.in,"Shift_JIS");
File f = new File("filename");
Reader fr = new FileReader(f);
Reader により文字の入力はできますが、通常のデータ処理で必要なのは文字 列です。 そのため、文字の入力を集めて取り出す java.io.BufferedReader クラスを使 います。 これは Reader オブジェクトをコンストラクタに指定してインスタンス化でき ます。 この java.io.BufferedReader には readLine メソッドがあり、直接行を文字列 で取り出すことができます。 ここまでが通常の入力文字列の取扱い方法です。
Reader r = new InputStreamReader(System.in);
BufferedReader br = new BufferedReader(r);
String input;
while((input = br.readLine())!=null){
/* input の処理 */
}
入力している文字列が単一の数を表しているのであれば java.lang.Double.parseDouble や java.lang.Integer.parseInt メソッドを 使って double 型や int 型の値を取り出すことができます。
double dData = Double.parseDouble("123.456");
int iData = Integer.parseInt("123");
一方、複数の数値が空白、改行、"," などで区切られていたらどのようにして 取り出せば良いでしょうか? このような文字列の表現のルールを文法と呼びます。 文字列の文法の解釈法などはコンパイラの発達に伴い深く研究されてきました。 この文法に関する詳しい話はデータ構造とアルゴリズム II で紹介します。 ここでは、単純にいくつかの区切り記号がある場合のみを考えます。
Java 1.4 から java.lang.String には split というメソッドが追加されまし た。これは(正規表現という)パターンを指定することで、文字列をパターンで 区切り、文字列の配列と返すものです。
"123,456,,789".split(",") == {"123","456","","789"}
"123a456ba789".split("[ab]") == {"123","456","","789"}
"123=====456===789".split("=+") == {"123","456","789"}
"123=abc=456bca=aa789".split("[=abc]+") == {"123","456","789"}
split メソッドの引数には区切り記号の文字列を入れます。 但し、複数の区切り記号がある場合には[]で括る必要があります。 また、空白などの 1 個以上の連続は通常はひとつの区切りと考えますが、そ の場合は区切り記号の後ろに+(プラス記号)を付けます。
この split を使って空白で区切られた数値を連続して読むことを考えます。 ここで、このパターンとして便利な文字クラスをひとつ紹介しま す。 それは空白文字を示す \s という記号です。これには空白の他、 TAB、改行、 改ページなど、通常画面上で空白になる文字全てを含んでいます。 そのため、区切り記号のパターンとして "\\s+" を指定すれば("" の中では \(バックスラッシュ) は二個で一つの\(バックスラッシュ)を意味することに注 意)、全ての空白などを取り除いて文字列を分解してくれます。
C 言語の scanf 関数では空白も改行も数値の区切りとして同じ意味に取りま す。 上記の \s+ 指定で文字列を分解する際は、同様の処理が可能になります。 そこで、 readLine で取得した文字列を一端改行記号を付けて、入力全部を一 つの文字列に納めます。 そして、 split("\\s+") で分解すれば、全ての空白や改行を取り除いて、文 字列の配列になります。 これを数値化すれば数値の配列が得られることになります。
import java.io.*;
class Rei {
private static String getAll(Reader r) throws IOException {
BufferedReader br = new BufferedReader(r);
StringBuilder sb = new StringBuilder();
String input;
while((input = br.readLine())!=null){
sb.append(input);
sb.append("\n");
}
return sb.toString();
}
private static int[] parseIntArray(String s){
String[] dataArray = s.split("\\s+");
int[] result = new int[dataArray.length];
for(int i=0; i<result.length ; i++){
result[i] = Integer.parseInt(dataArray[i]);
}
return result;
}
public static void main(String[] arg) throws IOException {
Reader r = new InputStreamReader(System.in);
int[] array = parseIntArray(getAll(r));
for(int i : array){
System.out.println(i);
}
}
}
このプログラムを実行し、数値を空白や改行で区切って入力し、 Windows で は Ctrll-Z、 Unix 系では Ctrl-D を入力すると、入力した数値を一行に一つ 表示します。
Java 5 より、 C 言語の scanf のようなフォーマットを決め打ちして読み込 む方式が追加されました。 java.util.Scanner は java.util.Iterator<String> を実装しているクラスで す。 java.io.InputStream や java.io.File のインスタンスをコンストラクタに与 えると、区切り記号をデフォルトでは "\\s+" として入力列を区分し、イ テレータと同様に要素の有無を hasNext() で判定し、要素を next() で取り 出します。 さらに、次の要素が整数として読み込めるか否かを hasNextInt() で判定し、 nextInt() で要素を整数として読み込みます。 同様に double 型に対しては hasNextDouble() と nextDouble() があり、他 の基本型に対して同様のメソッドがあります。
なお、コンストラクタには文字コードを与えることも出来ます。 さらに区切り文字の正規表現も useDelimiter メソッドで与えることが出来ます。
コンピュータで情報処理をする際、情報をグラフの形で抽象化して処理するこ とがしばしばあります。 そこで、コンピュータでグラフを表現するしかたを考えます。
プログラムへの入出力のために、単純に文字列としてのやりとりを考えます。 まず、グラフの頂点にはすべて名前が付けられているとします。頂点の名前の 集合を V とします。 すると、辺は二つの頂点の組み合わせで表せます。 辺の集合を E とすると、 E には (a,b) など、頂点の名前のペアが含まれる ことになります。 なお、有向グラフでは辺は (出発点,終着点) で表すことにします。
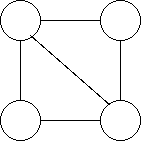
グラフは頂点と辺からなりますので、頂点の集合の要素と辺の集合の要素をそ れぞれ列挙すればグラフを表現できることになります。 下のグラフを要素の列挙で表現すると次のようになります。

頂点の数が n 個の時、n × n の正方行列を考えます。 もし、 i 番目の頂点から j 番目の頂点へ辺がある場合 (i,j) 成分を 1 に、 なければ (i,j) 成分を 0 にしたものはグラフの構造を表すことができます。 このような行列を 隣接行列 と言います。 なお、無向グラフで i と j に辺がある場合、 (i,j) 成分と (j,i) 成分をと もに 1 にします。

| a | b | c | d | |
|---|---|---|---|---|
| a | 0 | 0 | 1 | 0 |
| b | 1 | 0 | 1 | 0 |
| c | 0 | 1 | 0 | 0 |
| d | 0 | 0 | 1 | 0 |
さて、入力した数値から隣接行列を作ることを考えましょう。 ここでは単純のために、配列 array に対して、 array[0] に行列のサイズが 入っていて、その後は array[0]*array[0] 個の要素が入っているものとし、 int[][] 型の正方行列を返す関数を作ります。
private static int[][] getSquareMatrix(int[] array){
int n=array[0];
int[][] result = new int[n][];
int index=1;
for(int i=0; i<n; i++){
result[i] = new int[n];
for(int j=0; j<n; j++){
result[i][j] = array[index++];
}
}
return result;
}
なお、 java.util.Scanner を使用すると、次のようなシンプルなプログラム になります。
private static int[][] getMatrix(Scanner scanner){
int n = scanner.nextInt();
int[][] matrix = new int[n][];
for(int i=0; i<n; i++){
matrix[i] = new int[n];
for(int j=0; j<n; j++){
matrix[i][j] = scanner.nextInt();
}
}
return matrix;
}
この隣接行列を使ったサンプルプログラムとして、隣接行列から文字列の表現 に変換するプログラムを示します。
private static char getAlphabet(int i){
return (char)('a'+i);
}
private static String matrixToString(int[][] mat){
StringBuilder sb = new StringBuilder();
sb.append("V={");
boolean comma = false;
for(int i=0;i<mat.length;i++){
if(comma){
sb.append(",");
}
sb.append(getAlphabet(i));
comma = true;
}
sb.append("},E={");
comma=false;
for(int i=0;i<mat.length;i++){
for(int j=0;j<mat.length;j++){
if(mat[i][j]!=0){
if(comma){
sb.append(",");
}
sb.append("("+getAlphabet(i)+","+getAlphabet(j)+")");
comma = true;
}
}
}
sb.append("}");
return sb.toString();
}
オブジェクトのインスタンス変数として、自分自身の型を持ち、別のインスタ ンスを参照する形で、インスタンスを頂点、参照を辺として表す方法がありま す。

以下は、右のグラフを参照により表現し、その後文字列の表現に変換していま す。
import java.util.*;
class Node {
private String name;
private LinkedList<Node> edge;
public Node(String name){
this.name = name;
edge = new LinkedList<Node>();
}
public void addNode(Node n){
edge.add(n);
}
public String getName(){
return name;
}
public LinkedList<Node> getEdge(){
return edge;
}
}
class Rei {
private static String nodesToString(Node[] g){
StringBuilder sb = new StringBuilder();
boolean comma;
sb.append("V={");
comma = false;
for(Node n : g){
if(comma){
sb.append(",");
}
sb.append(n.getName());
comma = true;
}
sb.append("}, E={");
comma = false;
for(Node n : g){
for(Node e : n.getEdge()){
if(comma){
sb.append(",");
}
sb.append("("+n.getName()+","+e.getName()+")");
comma = true;
}
}
sb.append("}");
return sb.toString();
}
public static void main(String[] arg){
Node a = new Node("a");
Node b = new Node("b");
Node c = new Node("c");
Node d = new Node("d");
Node[] graph = {a,b,c,d};
a.addNode(c);
b.addNode(a);
b.addNode(c);
c.addNode(b);
d.addNode(c);
System.out.println(nodesToString(graph));
}
}
例9-1 のプログラムを使って、 5! と 6! を求めなさい。
例9-2 のプログラムについて以下の問いに答えなさい。
fibo(20)を求めなさい。
fibo(0)
から
fibo(50)
まで表示するプロ
グラムを作りなさい。
組合せの数を求める再帰的なプログラムを組みなさい。 そして、 5C2、 20C2 を求めなさい。
ハノイの塔において、 n 枚のディスクは何手で移動できるか、n の式を求め なさい。
頂点が 4 つの二分木は何種類あるか? 実際に作図して求めなさい。
表計算ソフトやデータベースソフトでは、古くから CSV(Comma Separated Value)というファイルフォーマットが使えるようになっています。 これは、行は CRLF(\r\n)で区切られていて、列は , (カンマ)で区切られてい るデータです。 以下は CSV のデータになります。
1,2,3 4,5,6
この他、文字列は""で括られるというルールがあります。 さて、表計算ソフトのデータを Java で活用するために、数値だけからなる CSV ファイルを double[][] 型に変換するプログラムを書きなさい。
次のグラフの隣接行列を求めなさい。

一筆書きができるグラフ(オイラーグラフ)である必要十分条件は、奇数の 次数を持つ頂点が 0 個か 2 個であることです。
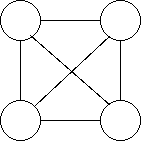
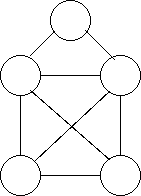
グラフの入力には隣接行列で入力するのが楽です。 最初に行列のサイズを入れ、そのあと、隣接行列を入力するようにします。
あたえられたグラフが連結グラフであるかどうか判定するプログラムを作りな さい。
隣接行列に対して and/or による行列の積を取ると、 k 乗が k 歩で行ける頂 点を表します。